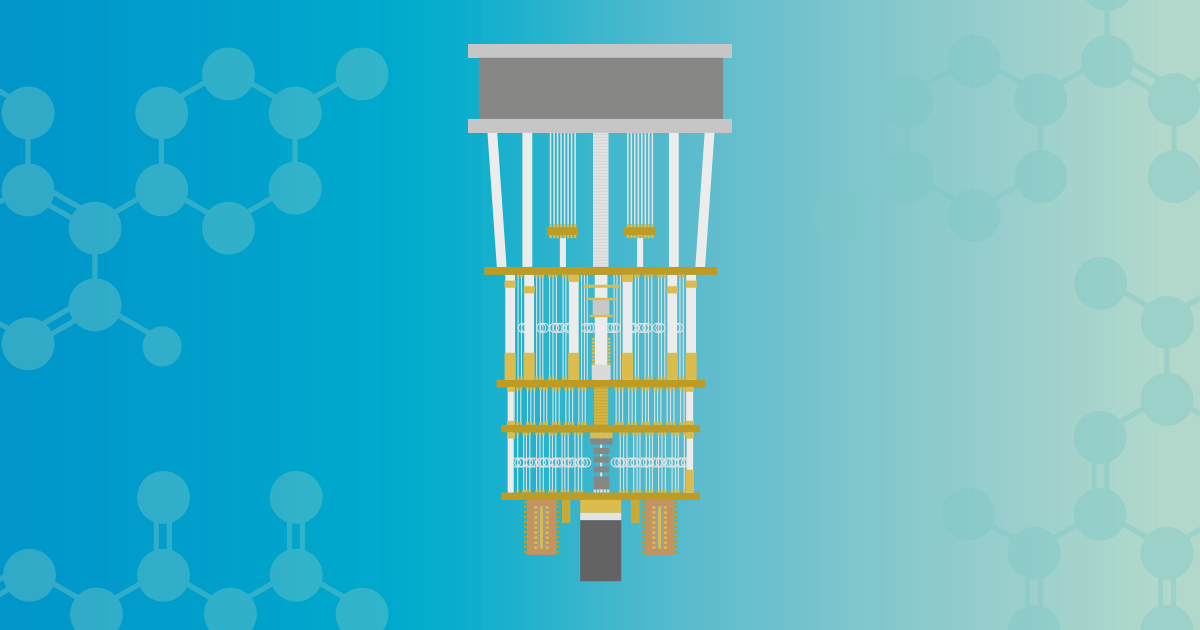
In my first article about quantum computers I explained the rudimentary principles. Now it gets a bit more concrete and practical. If you haven't read the first article yet, it would make sense to do so here before continuing.
Whatever works
What do you do when you've graduated with a PhD in your early 30s and have the idea of a "theory of everything" which is simple, aesthetic and logical? Something that could potentially secure you the highest honors in your field? Something that makes sure that you never have to pay for your own beer in any nerdy university pub ever again? Exactly, you turn your back on traditional science, state that your old professors suck, and go surfing in Maui, Hawaii. At least that's what this guy does:

Garrett Lisi mainly divides his time between surfing and working on his own revolutionary approaches to a new understanding of physics, which other physicists think is awesome and which he partly publishes here. There are three reasons you just have to know Garrett Lisi. Firstly, because he is the anarchist of the physicist community. Secondly, because his “Exceptionally Simple Theory of Everything” (or E8 Theory) could be what I already mentioned in my first article: the combination of all kinds of modern physics into one overall, smart-ass theory. Thirdly, because Lisi's work shows that the whole of quantum mechanics is based on the principle: The end justifies the means. Or to use the title of an iconic Woody Allen film: Whatever works.
And well, all quantum mechanical devices seem to work. Somehow. This is obvious because all digital electronics and modern communications are based on quantum mechanical principles. In fact, quantum mechanics is so far advanced that it can no longer be proven without the use of quantum mechanical stuff; a laser, for example. And yet: it is still experimental. What we don't know outweighs what we do know, and what we do know is derived from observations.
Qubits. Because normal bits are too 1980.
You already know the terms "superposition", "entanglement" and "interference". But these are all super-theoretical concepts. Let's put the whole thing into practice: the annoying quanta are still the core element to understand the functionality of a qubit (or quantum bit). The qubit is the quantum mechanical counterpart to the classical, digital bit, which is used for information processing, data transmission and storage in computers and data carriers. In close analogy to this world consisting of 0 and 1 we can describe the quantum-mechanical states with
|0⟩ and |1⟩.
Only with the sexy difference that a quantum is not exactly defined as there are superposition states (again: look at the first article). The quantum mechanical principle of superposition demands that there are infinite states of this system, which formally can be described as
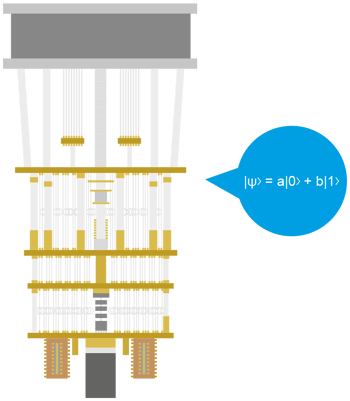
wherein a and b are complex numbers with:
|a|² + |b|² = 1
The probability of outcome |0⟩ with value “0” is |a|² and the probability of outcome |1⟩ with value “1” is |b|².
These sweet formulas may seem complicated, but when you write them on a window with a marker, you still won't be all Beautiful Mind. Because what they say is actually quite simple. Since quanta can be in both states at the same time, it is possible to perform massive parallel calculation steps with qubits. This so-called "quantum parallelism" can lead to an almost uncanny increase in performance.
Superposition means that there is no way to tell which of the two possible states forming the superposition state actually pertains. So the probability that a qubit is in state |0⟩ or |1⟩ is in most cases... unpredictable. And if you multiply this unpredictability, you get quite a lot of combinations.
These combinations are the unique selling point of the qubits. That's why they get away with their annoying ways.
Quantum computers test multiple solutions simultaneously
If a gate is applied to a qubit that is in a superposition, the change affects all states contained in it. This makes it possible to calculate with several input values. With one qubit, two actions are executed at once and with 14 qubits, for example, 16,384 values can be processed simultaneously.
This is the reason why a quantum computer can test several possible solutions to a problem at the same time. And this is also the biggest difference to classical computers: They process data step by step. It takes time for the final result to be achieved. There is only one solution at a time. On the other hand, the quantum computer stores all values at once. The result is one of these values and must be "filtered out".
Here we can also lead to the computational disadvantages of quantum computers - and to what they cannot do, at least at the moment, compared to a classical computer.
The clear disadvantage of a quantum computer with the already-described characteristics of the quantum world is that it is not deterministic. The correct result can achieve a higher probability of measurement than the others, but their probabilities do not have to drop to zero. The measured result can therefore be wrong, which is why the process must be repeated until you are sure you have the correct result. Of course, parallel computing is also possible with classical computers, but only with an increased expenditure of hardware as well as a high energy and space requirement. With quantum computers, the storage capacity doubles with every additional qubit. To crack an RSA code, however, several thousand entangled qubits are necessary. This is still a long way off.
What is "a lot of computing power"?
But to get an idea straight away: As far as quantum computers are concerned, there is no clear answer to how powerful they will be one day. However, how many qubits, or quantum bits, does the world's largest or most powerful quantum computer have? At the moment we are at about 72 qubits. This number is difficult to understand without a concrete context. The predecessor of this model had just 9 qubits, was incredibly powerful, but more importantly, it had such a high error rate that it was generally quite useless.
The 9 qubits quantum computer had an error rate of about 0.6 percent in logical operations of 2 qubits. The goal is not only to create quantum computers that delight us with a high qubit number. How powerful such a number is in reality, cannot (yet) be measured due to the high error rate. Therefore, the second goal is to have as low an error rate as possible. And not only in logical operations of 2 qubits (which, by the way, have the fancy name "quantum logic gate"), but with the inclusion of many qubits.
At some point scientists would like to reach the point where quantum computers are so powerful that they easily outdo every classical supercomputer. Interestingly, the last point is a kind of paradox. After all, it is precisely the classical supercomputers that have to test the reliability of quantum computations with a simulation so that we know that they are good for something. And that doesn't work anymore when the so-called "quantum supremacy" is reached (I didn't invent that word, it's a thing).
So, for the record: Quantum computers can potentially be a great deal. At the moment, however, they can do comparatively little in practical terms (aka "quantum impotence" - this word I invented).
Got a taste for it?
After two articles, are you really looking forward to trying it out for yourself? The bad news: It will probably be a few more years before people can sit in Starbucks with their first quantum computer and pretend they're writing the novel of the century. The good news: IBM Research is making a quantum computer publicly available for the first time. From now on, anyone interested can access a quantum processor consisting of five quantum bits via the IBM Cloud and carry out certain experiments using a desktop computer (or even mobile phone). Free access is intended to accelerate innovations towards the practical use of quantum computers.
The IBM Quantum Experience Platform offers users various ways to try out and discover quantum computing: they can test different algorithms and carry out experiments on the quantum processor, work with the individual qubits, and learn more about what quantum computers can do in online seminars and simulations. This quantum processor provided by IBM is located at the IBM T.J. Watson Research Center, IBM's research headquarters in Yorktown Heights, New York. The qubits were manufactured using a standard silicon technology process.
The IBM Research architecture used here allows scaling to larger quantum systems and is the leading approach to building a universal quantum computer. IBM plans to gradually add more qubits and new processor generations to the IBM Quantum Experience so that users can gain new experience and help discover new applications for this technology. With open access to the IBM Quantum Experience, companies and organizations can now begin to realize the potential of this technology. Universities will also have the opportunity to expand their curriculum in quantum computing and related areas with concrete application examples. And students will have the opportunity to familiarize themselves with promising new career paths in great degree programs with names like "Quantum Technology".
And if you already think that job titles are annoying today, then look forward to your team's new Quantum Technology Manager.
Oh, boy, the future...
 Published by
Published by